Any `fair market valuation’ of an employee-owned firm or partnership that assumes those future residuals accrue to the current shareholder/residual-claimants is inappropriate.
The Basic Ideas of Quantum Mechanics
September 19, 2025 by
For a century, quantum theorists have been reading the mathematical entrails of quantum mechanics (QM) to divine the nature of quantum reality. But to little avail. Let’s try a new approach.
The Mean and Variance as Dual Concepts
June 16, 2025 by
This paper gives a new derivation of the variance (and covariance) based on the two-sample approach, which positions the variance on the partition and information theory side of the duality and thus dual to the mean.
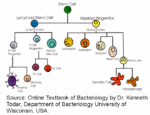
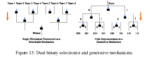
Generative Mechanisms
June 10, 2025 by
The purpose of this paper is to abstractly describe the notion of a generative mechanism
that implements a code and to provide a number of examples including the DNA-RNA machinery that
implements the genetic code, Chomsky’s Principles & Parameters model of a child acquiring a specific
grammar given ‘chunks’ of linguistic experience (which play the role of the received code), and embryonic
development where positional information in the developing embryo plays the role of the received code.
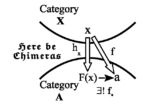
Where do Adjunctions come from?
March 19, 2025 by
Category theory has foundational importance because it provides conceptual lenses to characterize what is important and universal in mathematics—with adjunction seeming to be the primary lens. Our topic is a theory showing “where adjoints come from”.
Born Again! The Born Rule as a Feature of Superposition
March 18, 2025 by
Where does the Born Rule come from? We ask: “What is the simplest extension of probability theory where the Born rule appears”? This is answered by introducing “superposition events” in addition to the usual discrete events.
The heteromorphic approach to adjunctions: theory and history
March 15, 2025 by
In this paper, the history and theory of adjoint functors is investigated. Where do adjoint functors come from mathematically, and how did the concept develop historically?
A new logical measure for quantum information
March 15, 2025 by
Logical entropy is compared and contrasted with the usual notion of Shannon entropy. Then a semi-algorithmic procedure (from the mathematical folklore) is used to translate the notion of logical entropy at the set level to the corresponding notion of quantum logical entropy at the (Hilbert) vector space level.
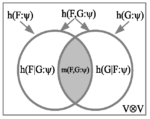
A Fundamental Duality in the Mathematical and Natural Sciences
September 8, 2024 by
This is an essay in what might be called “mathematical metaphysics.” There is a fundamental duality that runs through mathematics and the natural sciences, from logic to biology.